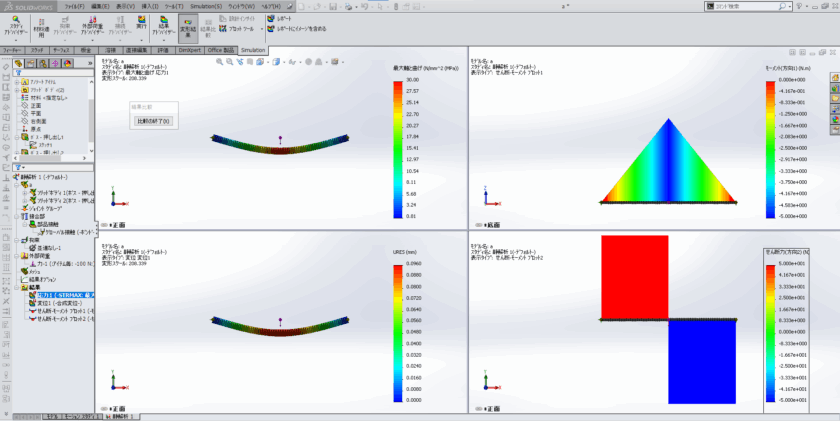
機械設計において、様々な部品の兼ね合いで変形が少なからず発生しています。
荷重の違いにより、引張り・圧縮・曲げなどの変形です。
変形が起こると部品内部に力が生じこれを内力と呼び、それを面積で割った値を応力と呼びます。
設計変更など寸法を変更しながら設計を進めるため、面積は変化する前提になるので、強度を考えるときには、応力をもとに比較検討していきます。
また、部品の公差の兼ね合いなどで想定の公差以上の変形が発生すると機械としての機能が損なわれる場合などもあるので、変形のしづらさを考えるため変位も検討対象になります。変形のしづらさを剛性とよびます。
垂直応力と変位
引張り応力と圧縮応力を総称して垂直応力と呼びます。
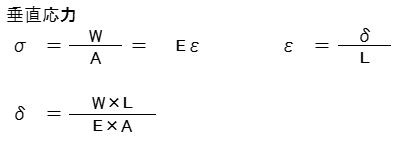
荷重をW[N]・断面積をA[mm2]として応力σ[MPa=N/mm2]を求めます。
また、縦弾性係数をE[103MPa]・部材長さをL[mm]として変位δ[mm]を求めます。
縦弾性係数は通常GPa単位なので公式はMPaに直す必要があります。
(縦ひずみε[無単位=mm/mm])
応力や変位の式の分母には面積が含まれています。これは、面積を大きくすると応力と変位が小さくなることを意味しています。
実際に強度計算を必要としない場合でもCAE解析を行う場合でもこの式の構成は把握しておくと寸法調整をするときの助けになります。
曲げ応力と変位
板上の部材の上に別な部材を乗せた場合などの時に曲げの変形が生じます。
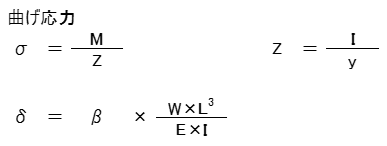
曲げモーメントをM[Nmm]・断面係数をZ[mm3]として応力σ[MPa=N/mm2]を求めます。
(曲げモーメントははりの種類や荷重によって変化します。)
また、断面二次モーメントをI[mm4]として変位δ[mm]を求めます。
(βはたわみ係数とよびはりの種類や荷重によって変化します。)
断面係数Z[mm3]と断面二次モーメントI[mm4]は断面形状によって式が異なります。
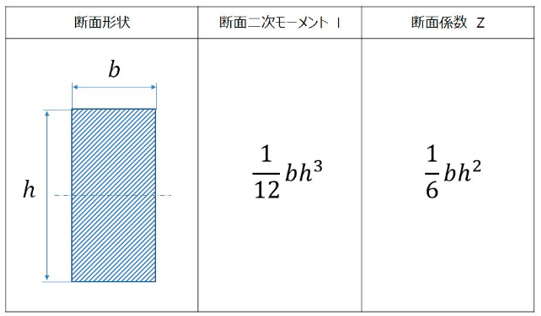
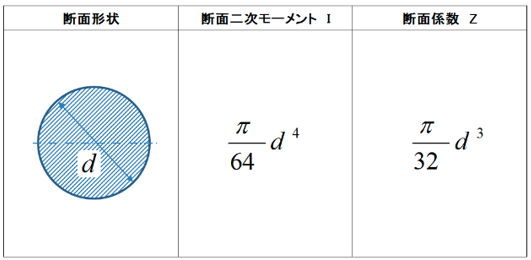
断面係数Z[mm3]は断面二次モーメントI[mm4]をyで割ったものになり、yはhの半分またはdの半分になります。
たわみ係数βや曲げモーメントMは、はりの種類や荷重の違いにより変化します。
代表的なはりと荷重に代入すると

というような式になります。
垂直応力と変位の式と類似しており、式の分母には面積に該当する断面係数Z[mm3]または断面二次モーメントI[mm4]が含まれています。
これは、断面係数Z[mm3]または断面二次モーメントI[mm4]を大きくすると応力と変位が小さくなることを意味しています。
集中荷重と等分布荷重を見比べると係数の値が変わり、同じ力なら点で受けるより面で受けた方が応力と変位は小さくなります。
片持ちはり・両端支持はり・両端固定はりを見比べると、順番に係数が小さくなっていき、両端固定はりが強度・剛性ともに強いことを指します。
実際に計算を必要としない場合でも力の受け方とはりの種類の特徴は設計時の参考になります。
逆に計算を必要とする場合に、両端支持と両端固定のどちらで計算したらいいか迷うようなケースでは、過剰品質になる恐れはありますが、両端支持の式を使うことで安全側に品質を保つことができます。
補足
応力や変位はCAEを用い線形静解析で行うことが多いですが、CAEの設定の可否を検証する場合は、公式から計算しておよその目安値を割り出す場合もあるのでよく使いそうな式はエクセルなどで作りこんでおくことをお勧めします。
断面積や断面二次モーメントなどは、複雑になれば計算に手間がかかるので、CADの種類によっては調べることができます。
フレームなど購入する場合もメーカーで断面二次モーメントを提示している場合もあるのでカタログなどを調べてみてください。
変形の種類には他にせん断やねじりがありますが、CAEではフォンミーゼス応力という形で計算をし、せん断応力は考えない場合が多いので今回は省略しています。